EXERCICI 1
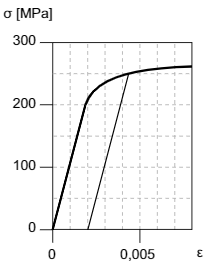
Qüestió 1: La figura mostra la corba tensió-deformació obtinguda en un assaig de tracció. Quin valor aproximat té el mòdul elàstic del material?
Qüestió 2: Un cotxe està equipat amb un motor de combustió interna de quatre cilindres en línia de 79,5mm de diàmetre i 80,5mm de cursa. Quina és la cilindrada del motor?
Qüestió 3: Una porta corredissa automàtica és accionada mitjançant un motor que gira a nmot=1500 min–1 i un reductor. L’eix de sortida del reductor és un pinyó de radi primitiu r=30 mm que acciona una cremallera fixa a la porta. En règim nominal, la porta es trasllada a una velocitat constant vnom=0,1 2m/s. Determineu la relació de transmissió entre la velocitat angular de l’eix de sortida del reductor i la velocitat angular de l’eix del motor τ=ωred/ωmot.
Qüestió 4: Es vol aixecar una massa m=1200 kg utilitzant una premsa hidràulica. La secció transversal de l’èmbol gran és de 30000 mm2 i la del petit és de 1000mm2. Quina força Fcal exercir sobre l’èmbol petit? (preneu g=9,807m/s2)
Qüestió 5: El Ti-6Al-7Nb és un aliatge biocompatible de titani àmpliament utilitzat en aplicacions quirúrgiques. Conté un 5,5% d’alumini (Al), un 6,5% de niobi (Nb), 0,25% de ferro (Fe), un 0,08% de carboni (C) i la resta és titani (Ti). En l’obtenció d’aquest aliatge, quina quantitat de niobi cal per a aliar-lo amb 250kg de titani?